First of all try to familiarize yourself with the formulae on integration and trigonometric identities Basic Integration
you can integrate an expression term by term
that is you can break up an integral of sum or difference of two expressions into sum or difference of two integrals
but do not do that with a product or quotient of two functionsbut integral of 2f(x) can be expressed as 2 * integral of f(x) since "2" is a constantDefinite Integrals (Integrals with limits)
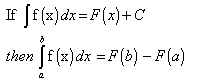
trying to write expressions in the form x^n
for eg.
cube root of x can be written as x^(1/3)
1 / (x ³) can be written as x^(-3)
if you know that the integral of f(x) is g(x) + C
then the integral of f(ax+b) will be ( 1/a ) g(ax+b) + C
you can divide the numerator term by term using the denominator but not the other way.if the numerator is of higher degree than the denominator use long division
if you have a product of sine and/or cosine terms use trigonometric identities for sinAcosB etc to break them into sum or difference before integrating
you can use substitution methods or trigonometric identities to evaluate integrals with powers of sine or cosines.
Examples on basic integration
integral of sin(5x)sin(8x)
answer and some explanation
integral of (x^3 +3x +4) /sqrt(x)
answer and some explanation
integral of [ x^3 - x^2 + x -1] / (x-1)
answer and some explanation
*integral of e^(2-3x) using limit of sums
answer of integral of e^(2-3x) using limit of sums
PAGE 1 BASIC INTEGRATION
PAGE 2 INTEGRATION BY SUBSTITUTION
PAGE 3 INTEGRATION BY COMPLETION OF SQUARES
PAGE 4 INTEGRATION BY PARTS
PAGE 5 INTEGRATION BY MANIPULATION OF NUMERATOR IN TERMS OF DENOMINATOR
PAGE 6 INTEGRATION USING PARTIAL FRACTIONS
PAGE 7 INTEGRATION OF 1 / [ACOSX +BSINX +C]
-----------------------------------------------------------
please leave your comments below
------------------------------------------------------------
index of math problems
disclaimer:
There is no guarantee about the data/information on this site. You use the data/information at your own risk. You use the advertisements displayed on this page at your own risk.We are not responsible for the content of external internet sites. Some of the links may not work
No comments:
Post a Comment
please leave your comments