solving a fourth degree equation with real coefficients if you are given one of the imaginary roots
solve x^4 - 4 x^3 + 11 x^2 -14x +10 =0 given that 1+2i is one of the roots.
since the coefficients of the given equation are real, the complex roots will occur in conjugate pairs
so 1-2i is another root.
using this you can find a quadratic factor of the given fourth degree expression.
use long division or comparision of coeffecients to extract the other quadratic factor and solve it
some questions in mathematics for the tamilnadu higher secondary 12th exam, isc , puc pre degree etc.
-----------------------------------------------------------
please leave your comments below
------------------------------------------------------------
index of math problems
disclaimer:
There is no guarantee about the data/information on this site. You use the data/information at your own risk. You use the advertisements displayed on this page at your own risk.We are not responsible for the content of external internet sites. Some of the links may not work

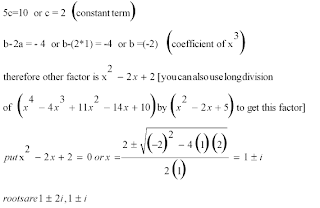
No comments:
Post a Comment
please leave your comments