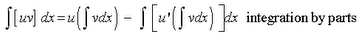
Integration formulae
If an integral is a product of the form uv
usually u is chosen so that successive derivatives of u will become zero after a finite number of stepsprovided v has a nice integral or you can make the choice using ILATE rule
inverse , log, algebraic, trigonometric, exponential
for eg. for integral of [x² cosx]
u = x² , v = cosx
but for integral of [x² ln(x)] , you should make it into integral of [ ln(x) * x²]
so that u = ln(x) , v = x²
for integral of lnx, make it into integral of [lnx * 1] with u = lnx , v = 1
in some integrals, like integral of [ (e^x) cosx ], take the integral as I, apply integration by parts a couple of times or so, and then obtain the original integral I again, then rearrange and extract the value of I.
also note the type
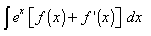
here split into two integrals
use integration by parts once on integral of [f(x)exp(x)] taking f(x) as the first function
this will cancel off the integral of [f '(x)exp(x)] leaving you with exp(x) * f(x ) + C which is the required answer
Examples on integration by parts
* integral of ln(x)
answer and some explanation
*integral of arc(cosx)
answer and some explanation
* integral of { [ arcsin(sqrt(x)) - arccos(sqrt(x)) ] / [ arcsin(sqrt(x)) + arccos(sqrt(x))] }
explanation and answer to the integral using integration by parts is available here
*integral of [1 / (x^4)][sqrt( 1 + (x^2))][ log( 1 + (x^2)) - 2log( x)]
explanation and answer using substitution and then integration by parts is available here
*integral of [e^2x]cos3x using integration by parts
explanation and answer of integral of [e^2x]cos3x using integration by parts
PAGE 1 BASIC INTEGRATION
PAGE 2 INTEGRATION BY SUBSTITUTIONPAGE 3 INTEGRATION BY COMPLETION OF SQUARES
PAGE 4 INTEGRATION BY PARTS
PAGE 5 INTEGRATION BY MANIPULATION OF NUMERATOR IN TERMS OF DENOMINATOR
-----------------------------------------------------------
please leave your comments below
------------------------------------------------------------
index of math problems
disclaimer:
There is no guarantee about the data/information on this site. You use the data/information at your own risk. You use the advertisements displayed on this page at your own risk.We are not responsible for the content of external internet sites. Some of the links may not work
No comments:
Post a Comment
please leave your comments